Answer ((Cos t)^2–3cost 2)/(sint)^2=1 If x= sint → (cost)^2=1x^2 The equation becomes ((1x^2)3√(1x^2)2 )/x^2=1 1x^2–3√(1x^2)2=x^2 3√(1x^2)= 2x^2–3 if X^2
Cos theta = 3/2-If $\sin^2 \theta 2\cos \theta – 2 = 0$, then find the value of $\cos^3 \theta \sec^3 \theta$ Stack Exchange Network Stack Exchange network consists of 180 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Cos theta root under 3 sin theta =2 then find the value of theta Get the answers you need, now!
Cos theta = 3/2のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  |  |
 |  |  |
「Cos theta = 3/2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「Cos theta = 3/2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  |  |
「Cos theta = 3/2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「Cos theta = 3/2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 | ||
「Cos theta = 3/2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | 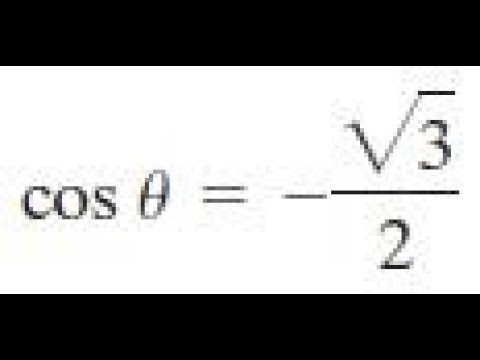 |
 |  | |
「Cos theta = 3/2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 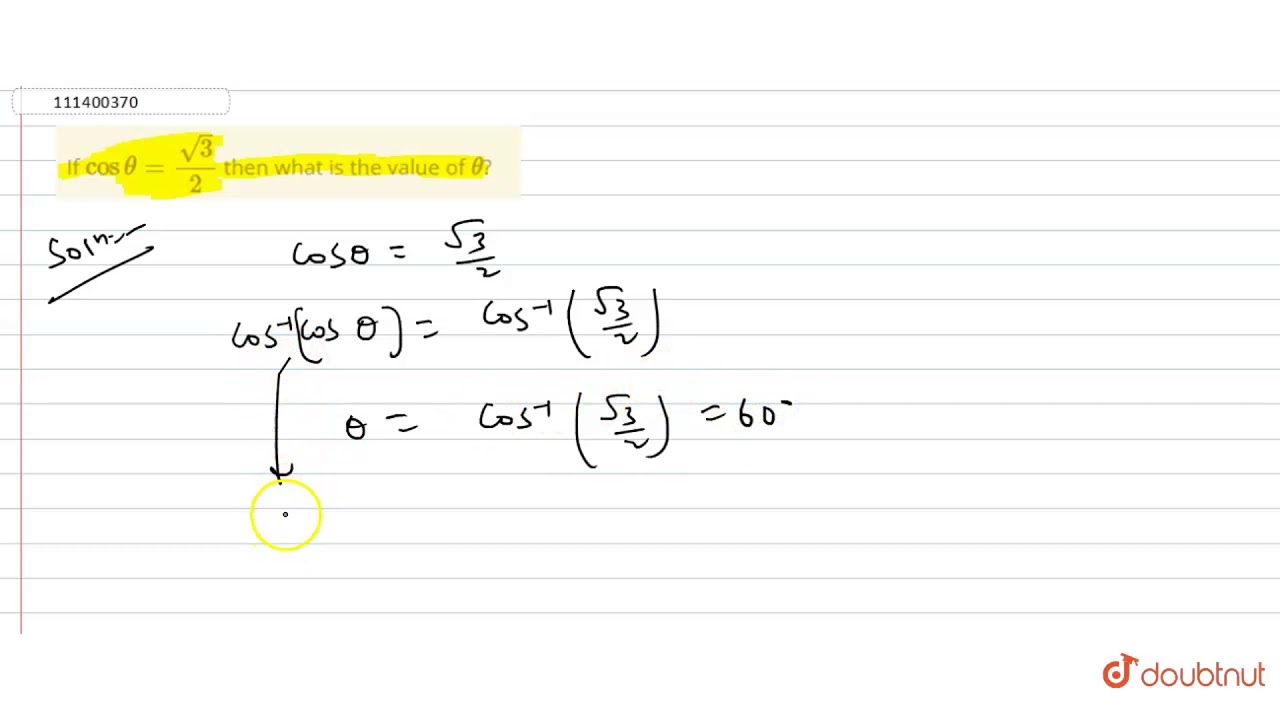 |
 |  |  |
 | ||
 | ||
「Cos theta = 3/2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「Cos theta = 3/2」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |
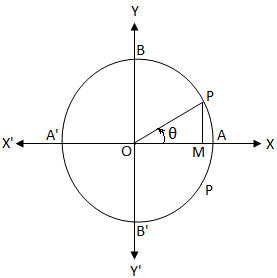
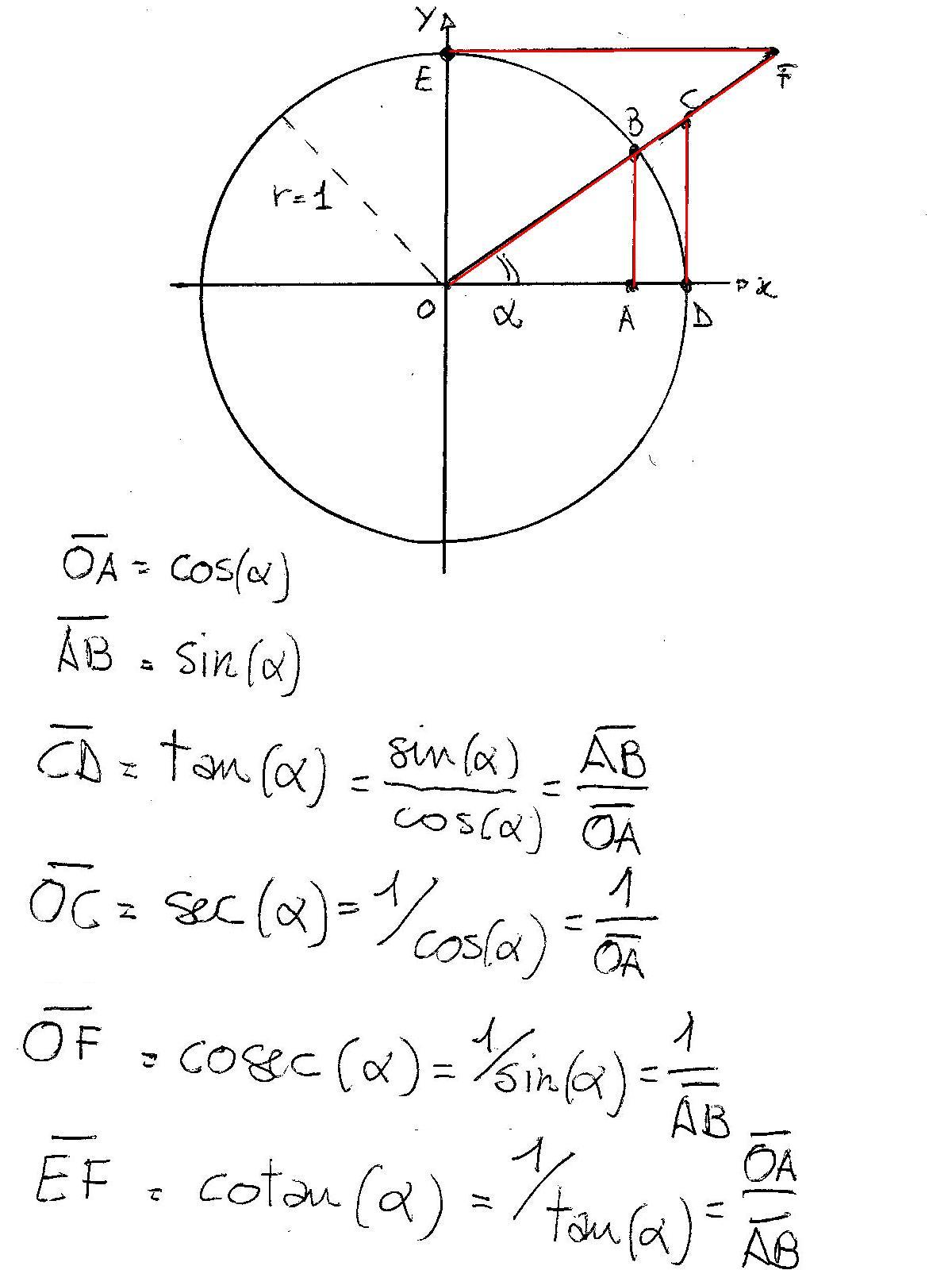
The Cos θ = Adjacent / Hypotenuse Cos angle formula There are many formulas in trigonometry but there are few most important basic formulas in trigonometry when it comes to a rightangle triangle The Cos theta or cos θ is the ratio of the adjacent side to the hypotenuse, where θ is one of the acute angles The cosine formula is as follows Explanation Here, cosθ = 2 3 > 0 ⇒ I stQuadrant or I V thQuadrant → (A) But, 180∘ < θ < 360∘ ⇒ I I I ndQuadran or I V thQuadrant → (B) From (A) and (B) ,we can say that 270∘ < θ < 360∘ → I V thQuadrant Hence, cosθ = 2 3 ⇒ θ = 360∘ − cos−1(2 3) = 360∘ −(4819)∘
Incoming Term: cos theta 3/2, cos theta = 3/2, cos x = sqrt 3/2, cos(θ+3/2π), cos x = 3/2, cos 3 theta/2cos2theta-1=, cos(x+3/2pi), cos x-3/2=0, cos theta = root 3/2, cos theta = - sqrt 3/2,




0 件のコメント:
コメントを投稿